Java 中的递归

递归

递归一种通过调用某个方法来描述需要重复进行的操作。该方法的特点就是可以自己调用自己。

案例一

排队的问题

在生活中，我们经常需要排队。排队时，我们怎么才能知道自己所排在第几位呢？

我们也许会想到数自己前面有几个人，这就是典型的迭代思想。就像是一个 while 循环，只要前面还有没数过的人，就不会停止。这种方式相对来说是比较直观的，但是同样也有局限性。比如在排队时，遇到了转弯，我们看不到前面的人怎么办呢？

有一个方法，我们可以通过询问前面一个人他所处的位置。假设有 A、B、C、D 四个人，D 询问 C 所在的位置，C 询问 B 所在位置，B 询问 A 所在的位置。A 知道自己排在第一位（他不需要再问别人了，这一个询问的过程结束），然后告诉 B，那 B 就知道自己在第二位；然后 B 告诉 C，C 也就知道了自己在第三位；最后 C 告诉 D 他在第三位时，D 也就知道自己所在的位置了。这就是使用递归思想来分析问题——每个人都来回答一个问题，从而使这个问题多次重现（recur）。

这一点也是递归思想的精髓所在，递归方法涉及多个进行合作的单元，每个单元负责解决问题的一小部分。例如刚刚那个例子，每个人都向前询问一个问题，最后每个人又向后回答一个问题，而不是由一个人来负责统计所有的人数。

迭代到递归的转变

根据传递的长度 length，打印出 length 个“ * ”

/**
 * 迭代
 *
 * @param length
 */
public void writeStars1(int length) {
    for (int i = 0; i < length; i++) {
        System.out.print("*");
    }
    System.out.println();
}

/**
 * 递归
 *
 * @param length
 */
public void writeStars2(int length) {
    if (length == 0) {
        System.out.println();
    } else {
        System.out.print("*");
        writeStars2(length - 1);
    }
}

上面这两个方法最终结果都是一样的。不同的是，迭代好比是一个人来统计所有的人数。递归则是由每个人回答同一个问题，由于每个人所在的位置不同，所回答的结果也不相同。

递归方法的结构

public void writeStars3(int length) {
    System.out.println("*");
    writeStars3(length - 1);
}

我们看一下上面这段代码，如果执行这段代码，程序并不会停止，会一直在自己调用自己执行下去。这也就是我们可能会遇到的 无穷递归（infinite recursion）。

递归方法有两个重要的组成部分：一个 基本情况 （base case）和一个 递归情况（recursive case）。

基本情况 一种简单到不需要递归调用就可以解决的情况。

递归情况 一种需要把整个问题转化成一个相同种类的，比较简单的，而且可以通过递归调用来解决的问题的情况。

/**
 * 通过注释来解释基本情况和递归情况
 *
 * @param length
 */
public void writeStars2(int length) {
    if (length == 0) {
        // 基本情况
        System.out.println();
    } else {
        // 递归情况
        System.out.print("*");
        writeStars2(length - 1);
    }
}

案例二

我们有一个 LinkedList 集合，现在需要按照倒叙把集合的内容打印出来，打印完之后集合里面不要有数据。

通过迭代实现

代码

LinkedList<String> list = new LinkedList<>();
list.add("a");
list.add("b");
list.add("c");
list.add("d");
list.add("e");
list.add("f");

System.out.println(list);

for (int i = list.size() - 1; i >= 0; i--) {
    System.out.print(list.get(i) + " ");
}
list.clear();
System.out.println();
System.out.println(list);

输出结果

1
2
3

[a, b, c, d, e, f]
f e d c b a 
[]

看到上面的结果，显然是符合要求的。那我们如果使用递归，该怎么实现呢？

通过递归实现

代码

public static void main(String[] args) {

    LinkedList<String> list = new LinkedList<>();
    list.add("a");
    list.add("b");
    list.add("c");
    list.add("d");
    list.add("e");
    list.add("f");

    System.out.println(list);

    Iterator<String> iterator = list.iterator();
    writeArray(iterator);

    System.out.println();
    System.out.println(list);
}

/**
 * 递归实现
 * @param iterator
 */
private static void writeArray(Iterator<String> iterator) {
    // 如果迭代器中还有数据，才进行递归计算
    if (iterator.hasNext()) {
        // 获得当前指针的参数
        String next = iterator.next();
        // 删除当前指针
        iterator.remove();
        // 使用递归计算
        writeArray(iterator);
        System.out.print(next + " ");
    }
}

输出结果

1
2
3

[a, b, c, d, e, f]
f e d c b a 
[]

由上述代码可以看出，使用递归算法，也可以同样得到结果，并且可以不使用 for 循环来完成任务。

调用栈

调用栈 用来跟踪所调用方法的顺序的内部结构。

了解递归的底层机制，对于初学者来说是很有帮助的。我们先来分析下面这段代码：

public static void main(String[] args) {
     draw();
     draws();
}

private static void draw(){
    System.out.println(" 在纸上画了一幅画 ");
}
private static void draws(){
    draw();
    draw();
}

我们来人工 debug 一下这段代码。

程序首先进入 main 方法；
然后程序会停止执行 main 方法，转而去执行 draw 方法，当程序执行完 draw 方法时，会回到 main 方法当中；
接着需要执行 draws 方法，draws 方法又会去调用两次 draw 方法。而此时位于顶端的方法则是我们正在执行的方法 draw；
当我们执行 draw 时，回到了 draws 上面，执行完 draws 后，最终会回到 main 方法中；

调用一个方法我们就把它放在最上面的位置，这就是 Java 的 调用栈（call stack）

了解了什么是调用栈，则可以利用调用栈来分析刚刚那个递归倒叙是如何工作的了。

案例三

整数的密运算 。Math.pow(x, y) 可以进行 x 的 y 次幂 运算。但是如果要通过递归该如何实现呢？

为求简单，我们只考虑整数的情况。也就是说我们不考虑负指数，因为它的结果不是整数。

在递归情况中，我们已知 y > 0。我们至少需要再乘一个 x：x 的 y 次幂=x * x 的 y-1 次幂（ $x^y = x * x^z$ ）。由此我们可通过以下代码实现。

public static void main(String[] args) {
    System.out.println(Math.pow(3, 5));
    System.out.println(pow(3, 5));
}

private static int pow(int x, int y) {
    // 按照定义，任何整数的零次幂都是 1
    if (y == 0) {
        return 1;
    } else {
        return x * pow(x, y - 1);
    }
}

运算结果

1
2

243.0
243

案例四

我们在写程序时，通常都会使用包含上下级结构的码表，例如下面这个数据：

SysCode{scId='01', itemName=' 测试 1', sort=1, fScId='null', cDesc=' 测试测试 1'}
SysCode{scId='02', itemName=' 测试 2', sort=1, fScId='01', cDesc=' 测试测试 2'}
SysCode{scId='03', itemName=' 测试 3', sort=3, fScId='01', cDesc=' 测试测试 3'}
SysCode{scId='04', itemName=' 测试 4', sort=2, fScId='01', cDesc=' 测试测试 4'}
SysCode{scId='05', itemName=' 测试 5', sort=1, fScId='03', cDesc=' 测试测试 5'}
SysCode{scId='06', itemName=' 测试 6', sort=2, fScId='03', cDesc=' 测试测试 6'}
SysCode{scId='07', itemName=' 测试 7', sort=2, fScId='null', cDesc=' 测试测试 2'}
SysCode{scId='08', itemName=' 测试 8', sort=1, fScId='07', cDesc=' 测试测试 2'}

分析以上代码，我们可以根据 fScId 封装上下级
关系，首先在 SysCode 类中增加一个 children 集合来保存子集。

/**
 * 使用递归创建子集
 *
 * @param scId
 * @param list
 * @return
 */
private List<SysCode> getSysCodeChildren(String scId, List<SysCode> list) {
    List<SysCode> sysCodeList = new ArrayList<>();
    list.forEach(e -> {
        if (null != e.getfScId() && e.getfScId().equals(scId)) {
            e.setChildren(getSysCodeChildren(e.getScId(), list));
            sysCodeList.add(e);
        }
    });
    return sysCodeList;
}

递归回溯

很多问题都可以通过系统地检查各种可能性来求解。比如，一个迷宫得游戏，要从入口找到出口，可以检查每一条线路，直到找到可行的线路。

很多使用穷举搜索求解得问题都能够用回溯法（backtracking）求解。回溯法是一种适宜用递归方式表示的问题求解方法。因此，这种方法也称为 递归回溯（recursive backtracking）。

（递归）回溯法 一种搜索问题解的通用算法，它先找出可能得候选解，一旦确定某个候选解不适合，就立刻放弃进一步尝试（回溯）。

案例分析

移动线路问题

考虑一个标准的平面直角坐标系（x, y），假设从原点（0, 0）出发，可以进行以下三种移动方式：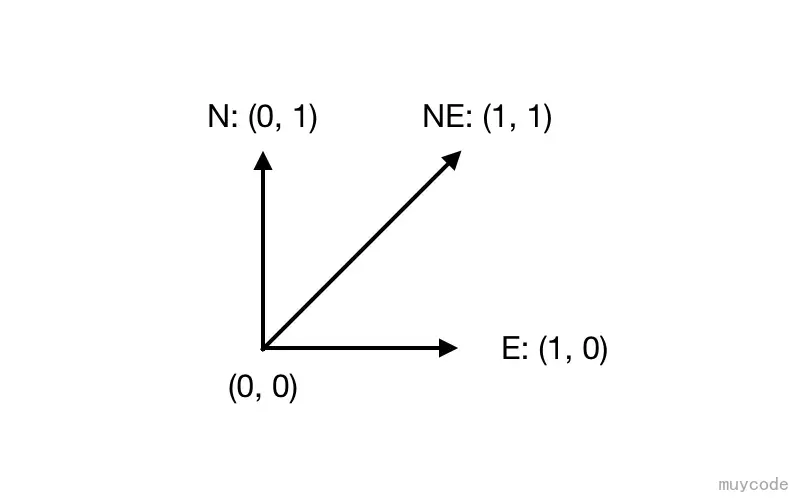
线路移动说明

向北移动（用“ N ”表示），每次移动纵坐标 +1；
向东移动（用“ E ”表示），每次移动横坐标 +1；
向东北移动（用“ NE ”表示），每次纵坐标，横坐标各 +1；

如上图所示，从原点出发，会有三种不同的移动方式。现在定义一种移动路线问题：通过一系列移动，从原点到坐标（x, y）。例如，通过移动序列：N -> NE -> N 可以到达（1, 3）。

每个适用于回溯法解决的问题都具有包含问题所有可能解的解空间（solution space）。可以把解空间想象成一颗决策树（decision tree）。对于我们要解决的移动线路问题来说，每次移动方案都是选择的结果。

决策树

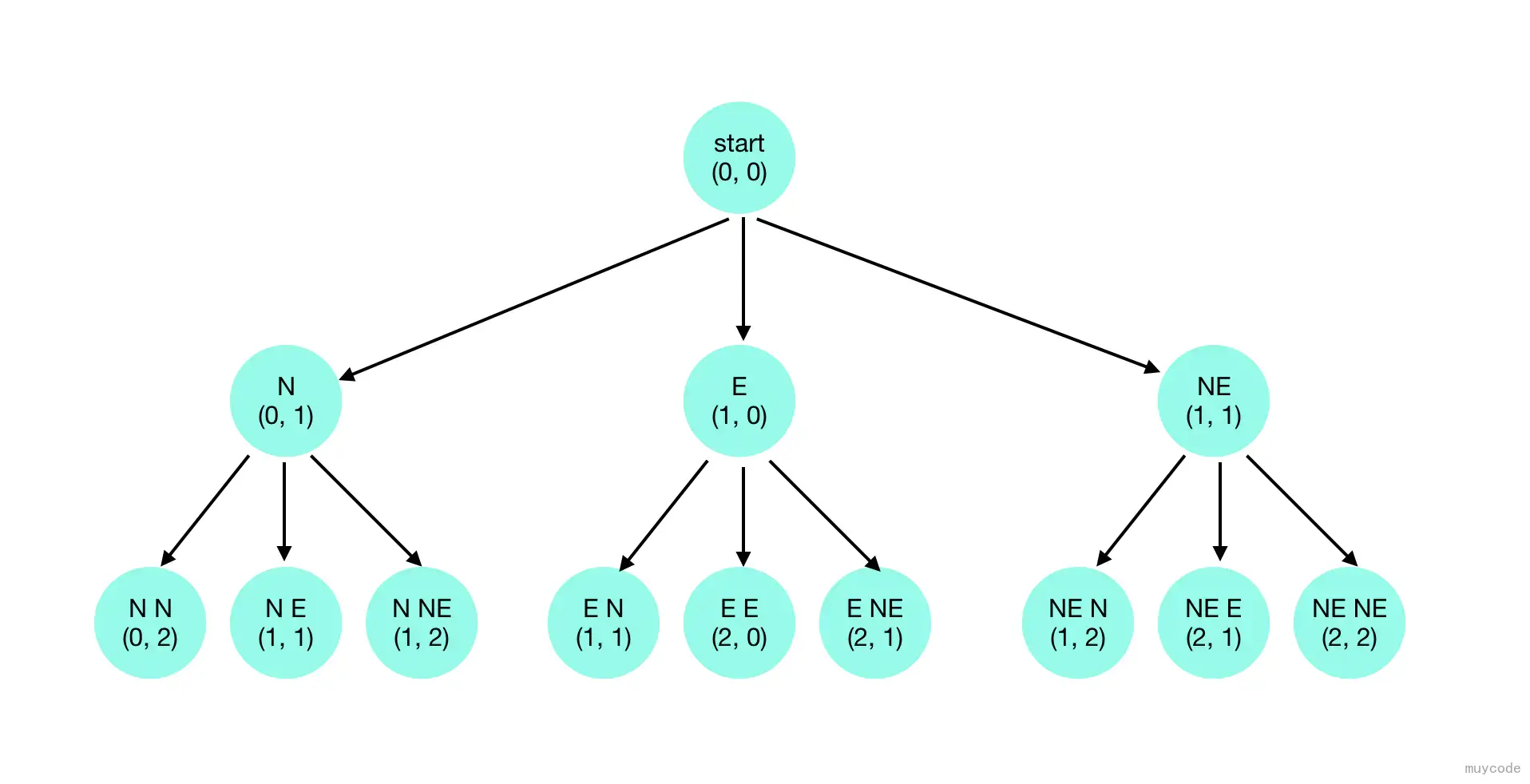
考虑从原点（0, 0）到（1, 2），所有可能的移动序号是：

N -> N -> E
N -> E -> N
N -> NE
E -> N -> N
NE -> N

用程序该如何找出这些解呢？对于大多数回溯问题，最终都会编写两个方法。一般会定义一个含有反应问题特性的参数的公有方法。另外会定义一个包含一些额外参数，执行实际回溯处理过程的私有方法。

因为要使用递归，所以需要确定基本情况和递归情况这两个部分。回溯法通常包含两种不通的基本情况。找到解时，停止回溯，这也是递归过程的一个基本情况。发现遇到死路的时候，停止继续搜索。

在回溯搜索过程中，如果既没有找到问题的解，也没有进入死路，就需要继续探索每一种可能的选择。根据上述的分析，我们可以编写以下伪代码来解释该回溯过程：

private static void explore(current(x, y), target(x, y)) {
    if(一个解) {
        打印出解
    } else if(不是死路) {
        explore(向 N 移动);
        explore(向 E 移动);
        explore(向 NE 移动);
    }
}

在这个问题中，我们需要当前位置的 x, y 坐标和目标 x, y 的坐标。还要记录每次移动的结果，用来形成最终的路径报告。

我们可以通过对比当前移动的起点和终点是否匹配，来验证是否找到了解。对于是否进入死路这个问题，我们知道在移动的过程中，横坐标和纵坐标只会递增，所以一旦当前位置的 x 坐标值大于目标位置的 x 坐标值，或者当前位置的 y 坐标值大于目标位置的 y 坐标值，就能知道在相应方向上移动距离超过了目标值，所以永远不可能找到解，这时需要停止继续搜索。整合这些分析，我们可以得到以下代码：

public static void main(String[] args) {

    // 使用回溯法找到（1, 2）的所有线路
    travel(1, 2);

}

/**
 * 反应问题特性的参数的公有方法
 *
 * @param targetX ：x 目标值
 * @param targetY ：y 目标值
 */
public static void travel(int targetX, int targetY) {
    explore(targetX, targetY, 0, 0, "path: ");
}

/**
 * 执行实际回溯处理过程的私有方法
 *
 * @param targetX ：x 目标值
 * @param targetY ：y 目标值
 * @param currX   ：当前 x 目标值
 * @param currY   ：当前 y 目标值
 * @param path    ：移动的路径
 */
private static void explore(int targetX, int targetY, int currX, int currY, String path) {
    if (currX == targetX && currY == targetY) {
        System.out.println(" 找到解：" + path);
    } else if (currX <= targetX && currY <= targetY) {
        explore(targetX, targetY, currX, currY + 1, path + " N");
        explore(targetX, targetY, currX + 1, currY, path + " E");
        explore(targetX, targetY, currX + 1, currY + 1, path + " NE");
    }
}

输出结果

找到解：path:  N N E
找到解：path:  N E N
找到解：path:  N NE
找到解：path:  E N N
找到解：path:  NE N

下图则是上述搜索对应的决策树，其中五个深色的部分就是找到的解。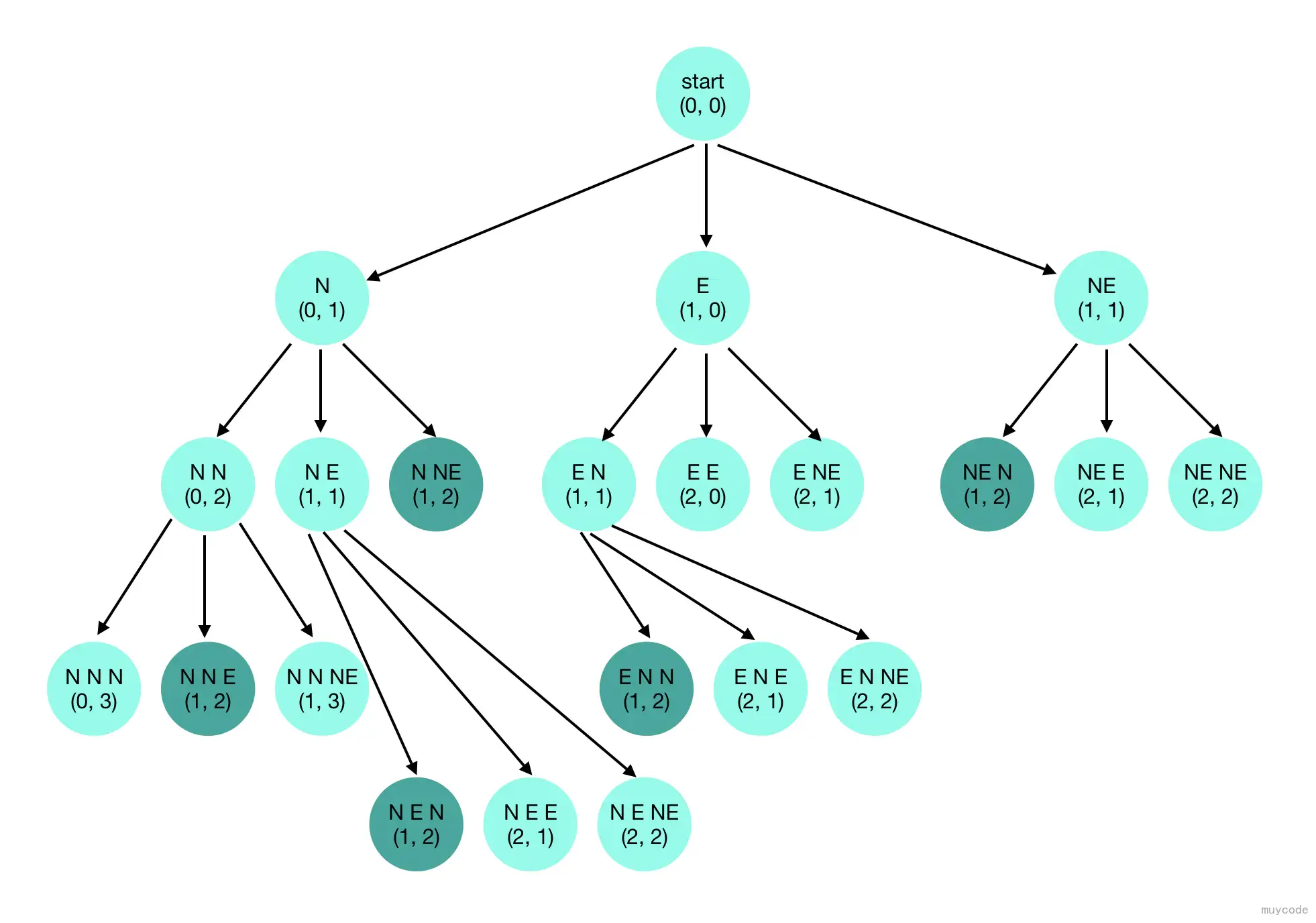
代码对应的决策树

这种返回到上一次选择并继续搜索其他可能性的特性，是讲该类方法成为回溯法的原因。找到解或者死路的时候，就返回上一次进行选择的情况，并尝试其他可能，直到尝试完所有可能的选择。

参考文章：

《Java 程序设计教程第三版》